Représentations des données polarimétriques dans le domaine de puissance
Il existe plusieurs représentations des propriétés diffusantes d'une cible, généralement dans le domaine de la puissance. Dans cette section, nous introduisons plusieurs représentations dans le domaine de puissance couramment utilisées.
- Matrice de covariance et matrice de cohérence
- Lissage des représentations de la puissance du signal
- Compression et format des données
- Matrices de Stokes et de Mueller
Matrice de covariance et matrice de cohérence
Le vecteur de diffusion, kC, également appelé vecteur de covariance, est une version vectorielle de la matrice de diffusion. Si l'on pose l'hypothèse de réciprocité (radars monostatiques), Shv = Svh, et on peut donc écrire :
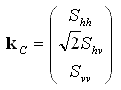. (2-1)
Il est utile de construire une représentation dans le domaine de puissance des propriétés diffusantes, ce que l'on réalise en multipliant le vecteur par lui-même. Ce produit est la matrice de covariance, laquelle donne une description complète des propriétés diffusantes de la cible. [
, section 5-4.10]:
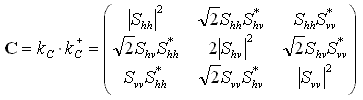, (2-2)
où « + » dénote le vecteur transposé conjugué et « * » le nombre complexe conjugué. La matrice de covariance est symétrique conjuguée.
Certains analystes préfèrent la matrice de cohérence, une forme proche de la matrice de covariance. On obtient la matrice de cohérence en vectorisant la matrice de diffusion à l'aide des éléments des matrices de spin de Pauli (en supposant ici encore la réciprocité) :
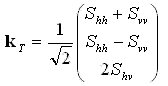. (2-3)
On préfère parfois ce vecteur parce que l'on peut donner une interprétation physique à ses éléments (écho impair, écho pair, diffusé, etc.). Notez que certains auteurs utilisent Svv - Shh comment deuxième élément pour le vecteur , mais obtiennent une analyse équivalente. Tout comme pour le vecteur précédent, on peut exprimer les informations contenues dans le vecteur kT en le multipliant avec lui-même pour produire la matrice de cohérence :
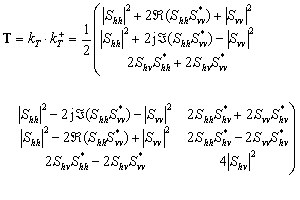(2-4)
Les matrices de covariance et de cohérence ont les mêmes valeurs propres, réelles. La somme des éléments diagonaux, la trace, des deux matrices est également identique et représente la puissance totale de l'onde diffusée, si l'onde incidente a une puissance unitaire. Notez que la plupart des auteurs utilisent la notation BSA (vers la cible) pour ces définitions.
Lissage des représentations de la puissance du signal
Lors de l'analyse des données des radars polarimétriques, il est utile de lisser les échantillons adjacents (remplacer les données par la moyenne de cette donnée et des échantillons adjacents). L'effet du lissage est analogue à la sommation des observations, dans le traitement de données de radar à synthèse d'ouverture dans une seule polarisation. Il réduit l'effet de bruit des tavelures (speckles), mais dégrade la résolution de l'image , .
Le saviez vous?
La matrice de diffusion d'un unique pixel, ne contient pas suffisamment de degrés de liberté pour représenter à la fois le bruit et les propriétés diffusantes de la cible, bien que l'observation contienne du bruit. C'est pourquoi, on doit supposer la présence d'un seul diffuseur, bien que le signal du pixel puisse provenir de plusieurs mécanismes de diffusion et contenir du bruit. Toutefois, après avoir converti les données en puissance et les avoir lissées, on obtient un pixel composite pour lequel on peut représenter explicitement le bruit et les différents mécanismes de diffusion.
Après le lissage, les diffuseurs ponctuels ne sont plus représentés par des échantillons distincts, mais seront " fondus " dans l'image. La réduction des tavelures et du bruit et le regroupement des signaux de diffusion ponctuelle, facilitent l'interprétation des images et rend la classification automatique plus sûre .
Puisque dans le domaine du voltage, le calcul de la moyenne ne conserve pas l'énergie, on doit effectuer le lissage dans le domaine de la puissance pour conserver l'énergie de chaque composante. Habituellement, on effectue le lissage après le traitement des données en calculant la moyenne des éléments correspondants de la matrice de covariance ou de la matrice de cohérence des échantillons adjacents. Le lissage a des avantages supplémentaires : il permet de réduire du volume de données et d'uniformiser l'espacement entre les pixels en distance sur le sol et en azimut.
Compression et format des données
Afin de traiter efficacement les données obtenues avec les radars polarimétriques AIRSAR et SIR C, les scientifiques du Jet Propulsion Laboratory (JPL) ont cherché un format simple et compact pour conserver et distribuer les données, tout en maintenant les informations essentielles pour leur interprétation et leur classification.
Le saviez vous?
Le saviez vous? La matrice de Stokes et la matrice de covariance contiennent de l'information sur la phase, bien qu'elles soient des représentations en puissance. En effet, les termes orthogonaux, comme sont des nombres complexes et l'« angle » du nombre complexe dépend de la différence de phase entre les canaux HH et VV.
Plutôt que d'entreposer les quatre éléments complexes de la matrice, ce qui pourrait exiger 32 octets par pixel, ils ont sélectionné la matrice de Stokes (Kennaugh) pour les données de AIRSAR et ont comprimé chaque échantillon (ou valeur moyenne d'un groupe d'échantillons) dans un mot long de 10 octets. D'autres systèmes de traitement compriment les données radar présentées sous la forme de la matrice de covariance , page 292.
Dans la méthode du JPL, la puissance totale de chaque échantillon est calculée et conservée dans deux octets, l'un pour la mantisse, l'autre pour l'exposant. On conserve les huit éléments uniques restants de la matrice de Stokes dans huit octets. Ces huit éléments sont normalisés par le premier élément de la première rangée, M11. On conserve la racine carrée des quatre éléments les plus petits qui contiennent les produits vectoriels des canaux de polarisation parallèle et de polarisation orthogonale. On peut facilement retrouver les éléments originaux de la matrice de Stokes à partir des valeurs conservées .
Lorsqu'il sera possible de conserver de très grandes quantités de données, on pourra conserver toute la matrice de diffusion (Sinclair) de chaque échantillon, sans devoir prendre la moyenne. On a mis au point des méthodes plus perfectionnées pour comprimer les données des images radar pour les données monocanal, notamment des méthodes utilisant la transformée DCT ou les ondelettes. Toutefois, on n'a pas encore testé complètement ces méthodes sur des données polarimétriques.
Question éclair
Question 1: Que signifie l'expression « mécanisme de diffusion »?
La réponse...
Question 2: Comment définit-on un « mécanisme de diffusion »?
La réponse...
Question 3: Pourquoi considère-t-on que la matrice de covariance est une représentation « en puissance »?
La réponse...
Question éclair - réponse
Réponse 1: Tout accident de terrain ou toute structure - plan d'eau, champ de maïs, ferme, automobile - disperse l'énergie du radar d'une façon qui lui est propre. On utilise les " mécanismes de diffusion " pour tenter de caractériser la diffusion d'une structure donnée à partir d'éléments simples dont on connaît les propriétés diffusantes ou que l'on peut modéliser, par exemple : la sphère, le dièdre, l'hélice et les diffuseurs composites, comme une distribution aléatoire de dipôles.
Réponse 2: Il existe deux méthodes fondamentales pour définir un « mécanisme de diffusion ». On peut premièrement élaborer un modèle physique du diffuseur, comme un dipôle ou un réflecteur trièdre, puis on utilise les principes physiques (notamment les équations de Maxwell) pour calculer comment les ondes électromagnétiques sont diffusées de la surface. La diffusion est décrite par la matrice de diffusion ou ses formes dérivées comme la matrice de Stokes ou la matrice de covariance. Le mot « mécanisme » fait référence au diffuseur élémentaire, ou modèle, et à la définition mathématique de son comportement diffusant.
La deuxième méthode consiste à faire une mesure directe de la diffusion, sur le terrain ou en laboratoire (dans une chambre anéchoïque par exemple). Dans ce cas, l'écho mesuré est habituellement formé par certains mécanismes élémentaires. On a créé différentes procédures mathématiques pour séparer le signal en composantes élémentaires (notamment, la décomposition en valeurs propres de la matrice de cohérence). Chaque composante est ensuite associée à un mécanisme de diffusion qui pourra, avec un peu de chance, être reliée à un des modèles physiques mentionnés plus haut.
Réponse 3: Puisque les éléments de la matrice de diffusion relient la « tension » de l'onde électromagnétique diffusée (l'intensité du champ électrique), à la « tension » de l'onde incidente, la matrice de covariance est formée de produits de ces éléments. En d'autres termes, la matrice de covariante relie la puissance de l'onde électromagnétique diffusée à la puissance de l'onde incidente.
Matrices de Stokes et de Mueller
Lorsqu'on utilise un vecteur de Stokes pour décrire la polarisation de l'onde incidente, Si, et un autre pour décrire celle de l'onde rétrodiffusée, Sd, la puissance rétrodiffusée par le diffuseur est définie par :
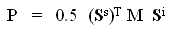(2-5)
où M est la matrice de Stokes, qui est un tableau 4 × 4 nombres réels. page 291, . En d'autres mots, la matrice de Stokes est une autre façon de transformer l'onde incidente en onde rétrodiffusée.
Lorsque l'on suppose qu'il y a réciprocité (radars monostatiques), la matrice de Stokes est symétrique, elle contient dix chiffres différents dont neuf sont indépendants. On peut en calculer chaque élément à partir de la matrice de diffusion.
La matrice de Mueller est proche de la matrice de Stokes, mais puisque l'on ne suppose pas la réciprocité, elle contient un plus grand nombre d'éléments indépendants. On utilise la matrice de Mueller avec la convention FSA (dans le sens de l'onde). Il existe une forme équivalente de l'équation de puissance (2 5) pour la matrice de Mueller, ainsi que pour les matrices de covariance et de cohérence.
La matrice de Kennaugh, K, est la version de la matrice de Stokes utilisée avec la convention BSA. Elles sont reliées par la relation M = diag[1 1 1 -1]K. La trace de la matrice de Kennaugh est égale à la puissance totale, ce qui n'est pas le cas pour la trace de la matrice de Mueller. On trouvera la définition des éléments de la matrice de Kennaugh dans .
Note : Les différents auteurs utilisent des noms différents pour désigner la matrice M (équation 2 5). Nous avons adopté la notation présentée par Raney à la page 119 du Manual of Remote Sensing . À la page 29 de leur livre , Ulaby et Elachi baptisent la matrice M, « opérateur de diffusion de Stokes ». Dans ce cours, nous avons adopté les conventions du Manual of Remote Sensing.
Détails de la page
- Date de modification :