Signatures polarimétriques

Étant donné toutes les polarisations que peut prendre l'onde incidente et puisque la matrice de diffusion comporte quatre nombres complexes, il est utile de disposer d'une méthode graphique permettant de visualiser la réponse d'une cible comme une fonction des polarisations incidentes et rétrodiffusées. Un de ces moyens est la signature polarimétrique de la cible .

On pourrait déterminer le pouvoir diffusant à partir des quatre variables de polarisation, des angles 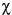et 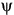de l'onde incidente et des angles 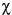et 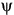de l'onde diffusée. Toutefois, le nombre de variables indépendantes est trop élevé pour pouvoir les observer. Pour simplifier l'exercice de visualisation, on limite l'observation des ondes rétrodiffusées à celles qui sont polarisées parallèlement ou orthogonalement à l'onde incidente. À partir de ce choix de combinaisons de polarisations, on peut calculer les réponses observées dans les canaux polarisés parallèlement et orthogonalement à chaque polarisation incidente, et les tracer comme deux surfaces, que nous appellerons ici « signature copolarisée » et « signature orthopolarisée ». Bien que ces deux signatures ne représentent pas toutes les combinaisons possibles de polarisations à l'émission et à la réception, elles nous donnent un modèle visuel utile des propriétés diffusantes de la cible , . On utilise habituellement la convention BSA pour le calcul de ces signatures.

On peut choisir une onde incidente dont l'ellipticité, 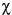, du vecteur du champ électrique est située entre -45° et +45° et son orientation, 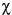and 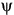, entre 0° et 180°. Ces variables constituent l'abscisse et l'ordonnée du graphique tridimensionnel de la signature polarimétrique. On calcule pour chacune des polarisations incidentes, la force de la rétrodiffusion dans la polarisation parallèle à la polarisation incidente (la signature copolarisée) et la polarisation orthogonale à la polarisation incidente (la signature orthopolarisée). Pour chaque onde incidente d'amplitude un, la puissance de la composante de l'onde diffusée dans la même polarisation (ou la polarisation orthogonale) est présentée comme une valeur de l'axe des z. Souvent les graphiques sont normalisés pour que la valeur maximale du signal soit égale à un.

Les graphiques de polarisation montrent des pics aux polarisations pour lesquelles la puissance reçue est maximale et des creux correspondant aux plus petites puissances reçues, en accord avec la fourchette de polarisation de Huynen sur la sphère de Poincaré. Les stations de travail conçues pour l'analyse polarimétrique, notamment les ordinateurs de bureau équipés du logiciel PWS, permettent de visualiser facilement la sphère de Poincaré. One example is the PWS software for PCs.

La figure 5-1 montre les signatures polarimétriques des cibles les plus simples : une grosse sphère conductrice, un plan uniforme et un réflecteur trièdre. L'onde est rétrodiffusée avec la même polarisation, sauf pour un changement du signe de l'ellipticité (ou, pour la polarisation linéaire, un saut de 180° de l'angle de phase entre E_h et E_v). Ce signe change à toutes les réflexions : l'onde rebondit une fois sur la sphère et trois fois sur le trièdre, donc ces deux diffuseurs se comportent comme un « réflecteur impair ».

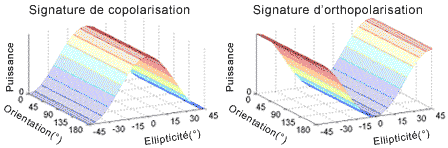
Figure 5-1 : Signature polarimétrique d'une grosse sphère conductrice ou d'un réflecteur trièdre.

La signature polarimétrique de cibles complexes possède une forme caractéristique. La réflexion sur un angle dièdre ou la diffusion de Bragg sur la surface de la mer ont des signatures particulièrement intéressantes. Dans le cas d'un déflecteur dièdre, lorsque la ligne d'intersection des deux côtés est alignée horizontalement, soit parallèlement à l'axe horizontal de l'onde électromagnétique, la réponse en polarisation parallèle est maximale pour les polarisations linéaire et elliptique horizontales, les polarisations linéaire et elliptique verticales ainsi que les polarisations circulaires. (Cf. figure 5 2). La deuxième réflexion sur la deuxième surface réfléchissante du dièdre annule le changement du signe de l'ellipticité et donne la signature typique du « réflecteur pair ».

Or, si nous tournons le réflecteur de 45° par rapport à la ligne de visée du radar, la « réponse » en polarisation parallèle horizontale est égale à zéro, alors que la réponse en polarisation orthogonale horizontale est maximale. À cause de cette propriété, on peut utiliser le dièdre comme un dispositif simple pour produire une « réponse orthopolarisée » d'un système de radar HH.

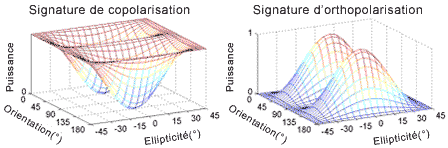
Figure 5-2 : Signatures polarimétriques d'un dièdre ou d'un réflecteur pair.

Dans le cas de la diffusion de Bragg, la réponse montre une crête analogue à celle d'une sphère (une seule réflexion), sauf que la rétrodiffusion de la polarisation verticale est plus intense que celle en polarisation horizontale (Cf. figure 5 3). La réponse en polarisation horizontale a un maximum pour une orientation = 90° et une ellipticité = 0° .

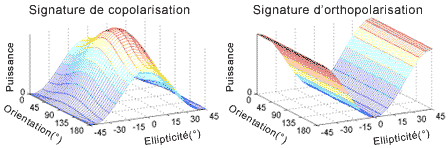
Figure 5-3 : Signatures polarimétriques de la diffusion de Bragg sur la surface de la mer (S_yy = 1.2*S_xx).

La hauteur du socle est un paramètre utile que l'on peut déterminer à partir des signatures polarimétriques. Elle est l'intensité minimale de la signature, une fois que l'on a normalisé la réponse maximale à un. La hauteur du socle est un indicateur de la présence d'une composante diffusée mais non polarisée de l'écho, il dépend du degré de polarisation de l'onde diffusée. Si une cible unique diffuse le signal radar et si l'onde rétrodiffusée est complètement polarisée ou si la signature est calculée à partir d'une seule mesure et non d'une moyenne, la hauteur du socle est nulle. Toutefois, si l'on calcule la signature à partir de la moyenne de plusieurs échantillons comportant plusieurs diffuseurs distincts ou encore si le signal reçu contient du bruit, la hauteur du socle ne sera pas égale à zéro. Donc, la hauteur du socle est une mesure du nombre de types différents de mécanismes de diffusion dans les échantillons dont on a calculé la moyenne.

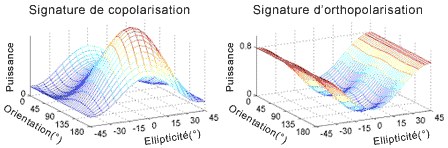
Figure 5-4 : Signature polarimétrique d'une cible dont la hauteur du socle est d'environ 0,2.

Whiz quiz

Question 1: Pourquoi la signature polarimétrique d'un réflecteur simple, une sphère par exemple, est elle en forme de crête? La réponse...

Question 2: La signature polarimétrique peut être « assise sur un socle ». Quelle est la signification de ce socle? La réponse...

Question 3: À quoi les signatures polarimétriques servent-elles surtout? La réponse...

Whiz quiz - answer

Réponse 1: La réponse copolarisée de toutes les polarisations incidentes est égale à un, alors que la réponse orthopolarisée est égale à zéro. Le changement de signe de l'ellipticité crée la crête - et la vallée - des graphiques des signatures. La réponse copolarisée est égale à un et la réponse orthopolarisée est égale à 0 pour toutes les polarisations linéaires (là où le changement de signe n'a pas d'effet). Toutefois, en polarisations circulaires - RR ou LL par exemple - la réponse en polarisation parallèle est zéro et elle est égale à un pour les polarisations orthogonales. Ce « changement de signe » dépend du choix de la convention pour les coordonnées. Nous avons choisi la convention BSA (vers la cible).

Réponse 2: La signature polarimétrique calculée à partir d'une seule observation (c.-à-d. un échantillon unique d'un système de radar polarimétrique) est une onde complètement polarisée, bien que cette mesure contienne plusieurs types de diffusion et du bruit. Ceci est causé par le fait qu'une observation unique ne possède pas assez de degrés de liberté pour être expliquée par autre chose qu'un seul mécanisme de diffusion. Puisque l'on suppose que l'onde diffusée est complètement polarisée, la signature sera égale à zéro pour au moins l'une des combinaisons de polarisation d'ondes émises et reçues.

Toutefois, lorsque l'on lisse les éléments des matrices de Stokes de pixels adjacents, la réponse nette contiendra les éléments de plus d'un type de diffuseur, ainsi que de bruit, pour peu que les matrices de Stokes ne soient pas toutes identiques . Dans ce cas, la valeur minimale de la signature polarimétrique ne sera pas zéro, mais une valeur positive donnée. La signature polarimétrique semble « flotter sur un socle ». La hauteur de ce socle dépend de la diversité des mécanismes de diffusion présents dans les pixels dont on a calculé la moyenne ou de la quantité de bruit présent dans les observations.

Réponse 3: Les signatures polarimétriques permettent de visualiser la réponse de rétrodiffusion d'une cible. On peut rapprocher la signature polarimétrique d'un pixel d'une image des signatures de cibles élémentaires connues et, ainsi, déduire le type de diffusion présent.

Lorsque l'on lisse les pixels d'une image, la réponse nette contient les composantes de plus d'un type de diffuseur, ainsi que le bruit. Ces composantes diffusantes sont additives lorsqu'on les analyse dans le domaine de puissance. Dans les cas favorables, on peut rapprocher la signature composite de signatures élémentaires connues et déduire le type de terrain présent dans l'image .