Algorithmes de classification

On classe habituellement les algorithmes de classification en méthodes dirigées et non dirigées, bien que certains algorithmes contiennent des éléments de chaque groupe. Dans les méthodes dirigées, un spécialiste classe les terrains présents dans une scène, ce qui permet de déterminer dans l'espace des paramètres, la moyenne ou les frontières qui définissent la classe. C'est ce que l'on appelle l'entraînement du logiciel. On peut choisir les données servant à l'entraînement dans la scène ou à partir de scènes analogues observées auparavant. Après l'entraînement, l'algorithme assigne automatiquement une classe à chaque pixel, à partir des moyennes ou frontières de classe prédéterminées.

Un algorithme de classification non dirigé ne contient aucune information préalable sur les éléments de la scène ou les classes de terrain qu'elle contient. L'algorithme analyse l'espace des paramètres de chaque scène et assigne des classes et des frontières à partir de groupements (ou nuages) de pixels. Parfois, on peut fonder les classes et les frontières sur des modèles physiques. Quel que soit le cas, l'opérateur doit intervenir pour identifier chaque classe après qu'elle a été assignée.

Les classificateurs dirigés ont le désavantage de nécessiter l'entrée d'information par l'opérateur et les classes qu'ils déterminent dépendent généralement de la scène. Les classificateurs non dirigés produisent souvent des classes dont l'interprétation physique est incertaine. Dans les prochains paragraphes, nous donnons un exemple de données de radar polarimétrique analysées par des classificateurs dirigés et non dirigés. Finalement, nous décrivons un nouveau classificateur qui combine des éléments des deux groupes de classificateurs.

Classification non dirigée fondée sur les paramètres H, A et α

L'utilisation correcte d'un classificateur dépend du choix des paramètres. Dans le cas de données polarimétriques radar, on peut utiliser des modèles de diffusion indépendants du contenu de la scène pour obtenir des paramètres qui permettront une distribution raisonnable en classes. Un bon exemple est l'ensemble des paramètres H, A et 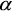que l'on peut calculer à partir des valeurs propres de la matrice de cohérence. On doit la création de l'algorithme H-A- 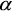à Cloude et Pottier qui ont démontré que les classes de terrain produisent parfois des groupements distincts dans le plan H -.

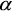La figure 7-1 montre un plan H-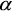. Les valeurs de l'angle a pour une valeur donnée d'entropie sont délimitées par les courbes I et II. Les régions ombrées sont interdites En effet, le fait de prendre la moyenne des différents mécanismes de diffusion (c.-à-d., pendre la moyenne des différents vecteurs propres) limite l'intervalle des valeurs que peut prendre a à mesure que l'entropie augmente. Le plan H- 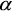est une représentation utile de l'information contenue dans la matrice de cohérence, puisque H et 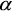sont tous deux des invariants quelle que soit la base de polarisation utilisée .

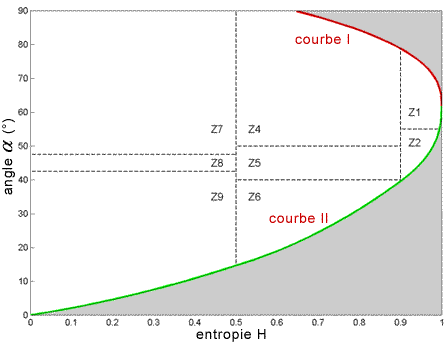
Figure 7-1 : Division des classes modélisées sur plan H-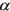. Le texte contient une description des neuf classes Z.

Les limites visibles à la figure 7-1 (courbes I et II) signifient qu'une entropie élevée limite beaucoup la capacité de classer les différents mécanismes de diffusion. La figure 7 1 montre un premier découpage effectué par Cloude et Pottier en neuf classes (dont huit utiles), choisies en fonction des propriétés générales des mécanismes de diffusion. Elles sont indépendantes des ensembles de données, ce qui autorise une classification non dirigée à partir des propriétés physiques du signal lui-même. Cloude et Pottier ont proposé une interprétation des neuf classes :

• Classe Z1 : double réflexion dans un environnement fortement entropique.
• Classe Z2 : diffusions multiples dans un environnement fortement entropique (tel le couvert forestier).
• Classe Z3 : diffusion de surface dans un environnement fortement entropique (région interdite du plan H-).
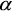• Classe Z4 : diffusion multiple dans un milieu modérément entropique.
• Classe Z5 : diffusion dipolaire (par la végétation), modérément entropique.
• Classe Z6 : diffusion de surface, modérément entropique.
• Classe Z7 : diffusions multiples, faiblement entropiques (réflexions doubles ou paires).
• Classe Z8 : diffusion dipolaire faiblement entropique (mécanismes fortement corrélés avec un déséquilibre prononcé en amplitude entre HH et VV).
• Classe Z9 : diffusion de surface faiblement entropique (par exemple diffusion de Bragg et surfaces irrégulières).

On notera toutefois que les limites sont passablement arbitraires et dépendent de l'étalonnage du radar, du bruit minimum des observations et de la variance des estimations des paramètres. Or, cette méthode de classification est liée aux caractéristiques physiques de la diffusion, elle n'est pas liée à un ensemble de données pouvant servir à entraîner un système. Le nombre de classes nécessaires, ainsi que l'utilité de la méthode dépendent de l'utilisation des observations. Une autre interprétation des classes est donnée dans , qui suggère un petit changement dans les frontières des classes.

On a utilisé la troisième variable, l'anisotropie polarimétrique, pour distinguer les différents types de diffusion de surface. La figure 7-2 montre le plan H-A, la région ombrée représente les valeurs pour lesquelles la diffusion de surface est impossible. On peut calculer la ligne qui délimite la région où la diffusion de surface est possible, à partir de la matrice de cohérence, en utilisant les valeurs propres mineures 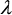₂ et 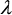₃, en faisant varier 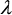₃ entre 0 et 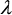₂.

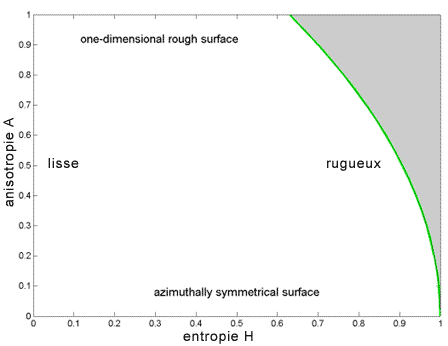
Figure 7-2 : Types de diffusion de surface dans le plan entropie-anisotropie.

L'ajout de l'anisotropie comme caractéristique nous donne un troisième paramètre que nous pouvons utiliser dans la classification. Une façon de le faire est de diviser simplement l'espace en deux plans H-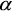-, le premier pour les valeurs de A inférieures ou égales à 0,5 et le second pour les valeurs de A supérieures à 0,5, ce que montre le plan de couleur verte coupant l'espace tridimensionnel de la figure 7-3. Nous obtenons alors seize classes, si nous conservons les divisions du plan H- 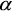montrées à la figure 7-1. On peut voir sur la figure 7-2 que la limite supérieure de H est restreinte pour les A supérieures à zéro.

L'espace de classification H-A-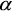, présenté à la figure 7-3, nous permet de mieux distinguer les divers mécanismes de diffusion. Par exemple, une entropie élevée avec une anisotropie faible (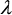₂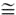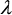₃) correspondent à une diffusion aléatoire, alors qu'une entropie et une anisotropie toutes deux élevées (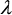₂ >> 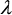₃) signalent la présence de deux mécanismes de diffusion également probables.

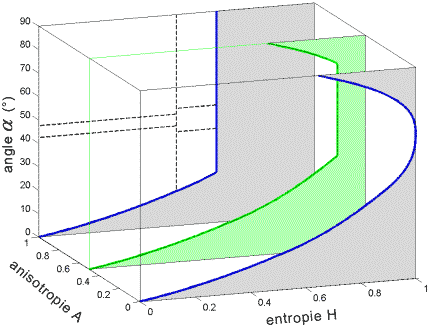
Figure 7-3 : Création de seize classes à partir des huit classes originales du plan H-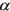 de la figure 7-1, par la division de l'espace H A 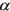à A = 0,5 (plan vert). On peut utiliser ces seize classes pour la classification non dirigée.

Les trois paramètres, H, A, et 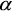sont calculés à partir des vecteurs et valeurs propres d'une estimation locale de la matrice de cohérence, laquelle est matrice hermitienne de trois rangées et trois colonnes. (Une matrice hermitienne est une matrice carrée à symétrie conjuguée 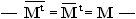, ses valeurs propres sont réelles.) À cause de l'invariance de la décomposition de la cible sous une transformation orthogonale, ces trois paramètres restent invariants en fonction de l'attitude. En d'autres termes, ils sont indépendants de la rotation de la cible relativement à la ligne de visée du radar, ce qui signifie aussi, que les paramètres sont les mêmes, quelle que soit la base de polarisation.

L'estimation des trois paramètres, H, A et 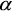permet de classifier la scène en fonction du type de processus de diffusion dans l'échantillon (H,A) et du mécanisme physique de diffusion correspondant, . On doit lisser les données afin d'estimer H, A et 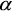(si on ne fait pas la moyenne, le rang de la matrice de cohérence est 1), ce qui permet de réduire le bruit de tavelure .

La figure 7-4a montre un exemple de regroupement de pixels, dans une scène de glace marine observée par SIR C. Le plan H-A montre des signes de groupement en deux classes, possiblement trois. La figure 7-4b montre la distribution des valeurs (H,A) pour un peuplement d'épinettes blanches. La diffusion dipolaire (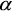 ~ 45°) domine la cible, la forte valeur de l'entropie (H ~ 0,8) indique que la diffusion est plutôt hétérogène. On a produit la figure 7-4b avec une station de travail PWS du Centre canadien de télédétection.

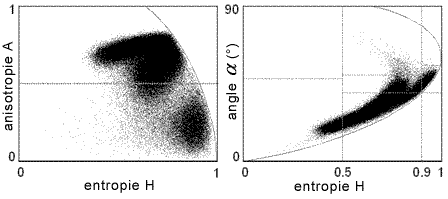
Figure 7-4a : Nuage de points dans l'espace de classification H-A- montrant la distribution des observations de glace marine obtenues avec le radar SIR-C. (Scheuchl)

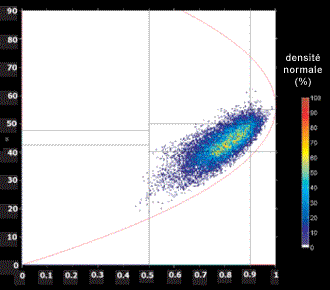
Figure 7-4b : Nuage de points dans l'espace de classification H-A- montrant la distribution des observations de glace marine obtenues avec le radar SIR-C.

Classification dirigée fondée sur la vraisemblance maximale de Bayes

On peut substituer aux méthodes fondées sur des modèles, la définition de classes calculées à partir de l'image elle-même. Ces classes sont définies par un opérateur qui choisit des plages représentatives de la scène pour définir la valeur moyenne des paramètres de chaque classe reconnaissable (il s'agit donc d'une méthode dirigée). On utilisera avec profit une approche statistique quand la production des données est en bonne partie stochastique. La connaissance des statistiques des données (c'est à dire la distribution statistique théorique) permet d'utiliser une approche de classification basée sur la vraisemblance maximale de Bayes. Cette approche est optimale, la probabilité d'erreur de classement est, en moyenne, la plus basse de toutes les méthodes .

Une fois que l'on a défini les statistiques de classes, les échantillons de l'image sont classés en fonction de leur distance de la moyenne de la classe. On assigne à chaque échantillon la classe dont il est le moins éloigné. L'échelle des distances est calculée à partir de la règle de la vraisemblance maximale de Bayes.

C'est en 1988, que l'on a présenté cette méthode de classification des données polarimétriques tirées de radar à synthèse d'ouverture . Ses auteurs ont démontré que l'utilisation de l'ensemble complet des données polarimétriques garantissait une classification optimale. Toutefois, l'algorithme n'a été mis au point que pour les images radar singulières (ou mono-impulsion). Dans la plupart des cas en télédétection par radar, on obtient des données plurielles (données multivisées) pour réduire les effets du bruit des tavelures. Le nombre de visées est un paramètre important pour la création de modèles probabilistes.

The full polarimetric information content is available in the scattering matrix S, the covariance matrix C, as well as the coherency matrix T. It has been shown that T and C are both distributed according to the complex Wishart distribution . The probability density function (pdf) of the averaged samples of T for a given number of looks, n, is

Toute l'information polarimétrique est contenue dans la matrice de diffusion, S, la matrice de covariance, C, et la matrice de cohérence, T. On a démontré que les matrices T et C sont distribuées selon une distribution de Wishart complexe. La fonction de densité de probabilité de la moyenne des échantillons de T pour un nombre donné de visées, n, est :

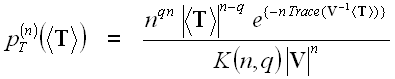, (7.1)

où

• <T> est la moyenne des échantillons de n visées de la matrice de cohérence,
• q est la dimensionnalité des données (3 s'il y a réciprocité, 4 pour les autres cas),
• Trace() est la somme des éléments diagonaux d'une matrice,
• V est la valeur espérée de la moyenne de la matrice de cohérence, E{<T>},
• K(n,q) est un facteur de normalisation.

Pour établir les statistiques de classification, on doit calculer la valeur moyenne de la matrice de cohérence pour chaque classe, V_m :

, (7.2)

où _m représente l'ensemble des pixels de la classe m dans les données qui ont servi à l'entraînement du classificateur.

Selon la classification de vraisemblance maximale de Bayes, on peut calculer la distance d, à partir de :

(7.3)

où le dernier terme tient compte des probabilités a priori, P(?_m). L'accroissement du nombre de visées, n, diminue la contribution de la probabilité a priori. Toutefois, si l'on ne dispose d'aucune information sur les probabilités des classes pour une scène donnée, on peut supposer que les probabilités a priori de toutes les classes sont égales à zéro. Dans ce cas, on peut définir une mesure appropriée de la distance :

(7.4)

ce qui nous donne un classificateur de distance minimale indépendant du nombre de visées :

(7.5)

Pour appliquer cette règle, on assigne un échantillon de l'image à une classe donnée, si la distance entre les valeurs des paramètres de cet échantillon et la moyenne de la classe est minimale. Puisque cette méthode est indépendante du nombre de visées, on peut l'utiliser pour des données multi-visées ou des données dont on a filtré les tavelures . On peut aussi généraliser cet outil de classement aux données multifréquences pour toutes les polarisations, si les fréquences sont suffisamment espacées pour assurer une indépendance statistique entre les bandes de fréquence .

La classification dépend de l'ensemble de données utilisées pour l'entraînement et doit donc être dirigée. Elle ne repose pas sur la physique des mécanismes de diffusion, ce qui peut constituer un désavantage. Elle exploite toutefois toute l'information polarimétrique et permet une classification des images indépendante du nombre de visées.

On peut aussi utiliser la méthode de classification de Bayes avec des données présentées sous la forme matrice de covariance. Nous avons utilisé la matrice de cohérence par souci d'uniformité avec notre présentation du classificateur H-A- (cf. section précédente).

Un algorithme de classification mixte

Les méthodes dirigées et non dirigées que nous avons décrites plus haut ont chacune leurs faiblesses. Les seuils de la classification H-A-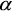 sont assez arbitraires et cette méthode n'exploite pas toute l'information polarimétrique, puisque l'on ne peut déterminer les quatre angles qui paramétrisent les valeurs propres. La technique de vraisemblance de Bayes exige l'utilisation d'un ensemble pour l'entraînement du programme ou un regroupement initial des données. Toutefois, chaque algorithme permet de combler les faiblesses de l'autre.

Une combinaison des deux algorithmes semblerait intéressante . On obtiendra une meilleure classification en appliquant d'abord le classificateur H-A-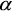 non dirigé pour isoler et regrouper les 16 classes initiales, puis le classificateur à distance minimum, sur la base de la distribution des paramètres des regroupements. On pourra utiliser la distribution de Wishart complexe et des itérations pour optimiser les limites entre les classes , , .

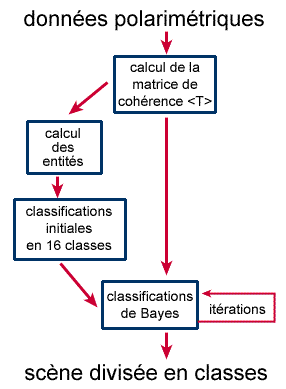
Figure 7-5 : Classificateur combiné H A 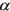- distance minimum.

L'algorithme combiné est illustré à la figure 7-5. On peut le considérer comme un algorithme non dirigé, puisque la classification initiale n'est pas dirigée. Toutefois, puisque les itérations raffinent les moyennes et les frontières des regroupements, il est recommandé d'examiner les classes finales et de leur attribuer une description correspondant à une interprétation physique. On notera que bien que le regroupement initial ait été effectué dans l'espace H-A-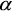, la classification suivant la distance minimum est réalisée en utilisant directement la matrice de cohérence. Après la classification de Bayes, il est possible que les regroupements se chevauchent dans l'espace H-A-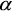. Puisque les résultats rendus par les classificateurs dépendent du nombre et de la diversité des classes déterminées à l'entrée du classificateur, il est toujours utile d'essayer plusieurs classes initiales.

La figure 7-6 donne un exemple des résultats de la méthode classification combinée. On a pu extraire de cette image prise par l'instrument SIR-C, en avril 1994, au large de la côte occidentale de Terre Neuve, quatre types de glace de mer, trois classes d'eau et quatre classes de terrain . Le degré de détails des types de glaces extraites est une indication de la puissance de la classification automatique des données polarimétriques.

Les algorithmes de classification peuvent contenir un algorithme de segmentation qui regroupe les pixels dont les caractéristiques sont communes avant de leur assigner une classe. Si elle est réalisée correctement, la segmentation pourra améliorer nettement les résultats de classification .

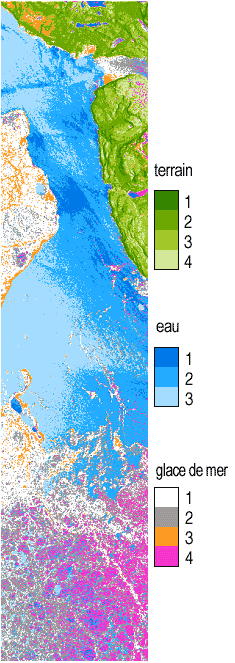
Figure 7-6 : Classification du terrain, de la mer et de la glace, dans une scène observée dans la bande C par le radar polarimétrique SIR-C, au large de la côte occidentale de Terre Neuve .