- Ondes électromagnétiques
- Diffusion polarimétrique
- Polarisations d'un système radar
- Matrice de diffusion
- Ellipse de polarisation
- État de polarisation
Ondes électromagnétiques
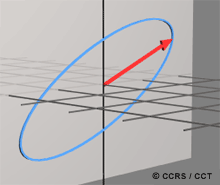
Une onde électromagnétique plane est constituée d'un champ électrique et d'un champ magnétique mutuellement orthogonaux qui oscillent dans le plan perpendiculaire à la direction de sa propagation  . Les ondes électromagnétiques sont décrites par les équations de Maxwell. Ces champs se déplacent à la vitesse de la lumière dans le vide et dans l'air - pour la plupart des conditions atmosphériques. Trois paramètres permettent de décrire complètement la propagation des ondes électromagnétiques dans un milieu donné : la constante diélectrique (ou permittivité), la perméabilité et la conductivité.
. Les ondes électromagnétiques sont décrites par les équations de Maxwell. Ces champs se déplacent à la vitesse de la lumière dans le vide et dans l'air - pour la plupart des conditions atmosphériques. Trois paramètres permettent de décrire complètement la propagation des ondes électromagnétiques dans un milieu donné : la constante diélectrique (ou permittivité), la perméabilité et la conductivité.
En général, une onde électromagnétique émise d'une source - une antenne radar par exemple - se propage dans toutes les directions avec, pour chaque direction, une intensité et une phase particulières. À une grande distance de l'antenne, on peut supposer que le front d'onde est plan, plutôt que sphérique. Puisque nous ne sommes intéressés qu'à ce qui arrive à l'onde le long d'une trajectoire donnée, l'hypothèse de l'onde plane est valide.
 Saviez-vous que?
Saviez-vous que?
La composante prévisible d'une onde électromagnétique montre une structure géométrique caractéristique qui définit ses propriétés polarimétriques. Si on pose des axes horizontal et vertical relativement à un système de coordonnées particulier (par exemple les axes définis parallèlement aux long et petit côtés de l'antenne radar), la pointe du vecteur du champ électrique décrit une courbe régulière, lorsqu'on l'observe le long de la direction de sa propagation. La longueur et le taux de rotation du vecteur sont respectivement l'amplitude et la fréquence de l'onde. La polarisation réfère à l'orientation et à la forme de la courbe tracée par la pointe du vecteur. Nous en discutons dans la prochaine section.
La polarisation est une propriété importante de l'onde électromagnétique. La polarisation décrit l'alignement et la régularité des champs électriques et magnétiques de l'onde dans le plan transverse à sa propagation. Par convention, on s'intéresse à la composante électrique des champs de l'onde puisque, selon les équations de Maxwell, elle précède le champ magnétique orthogonal. (Le champ magnétique est directement lié au champ électrique et on peut toujours le calculer à partir de ce dernier.) C'est pourquoi on peut représenter l'onde électromagnétique en décrivant seulement la variation du champ électrique en fonction du temps. La figure 1.1 montre la propagation d'une onde électromagnétique.
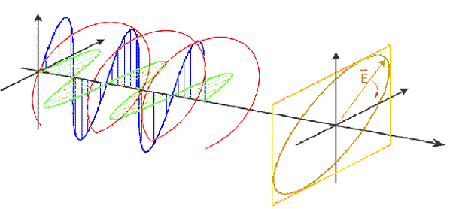
Figure 1-1 La ligne tracée par la pointe du vecteur du champ électrique (en rouge) est la résultante de ses composantes horizontale (en vert) et verticale (en bleu). Le lieu tracé par la pointe du vecteur du champ électrique (en kaki) montre un cycle complet de l'onde dans le plan perpendiculaire à sa propagation. (Avec la permission de Martin Hellmann, http://epsilon.nought.de/.)
La forme de l'onde du vecteur du champ électrique peut être prévisible, aléatoire ou combiner les deux. Une composante aléatoire est analogue à un bruit pur : ni sa fréquence ni la forme de son amplitude ne sont définies. Un exemple de composante prévisible est une onde sinusoïdale monochromatique dont la fréquence et l'amplitude sont constantes. On dit d'une onde électromagnétique qui n'a pas de composante aléatoire qu'elle est « complètement polarisée ».
Diffusion polarimétrique
Nous avons donné une représentation de l'onde polarisée et sommes maintenant prêts à décrire la diffusion par une cible d'une onde électromagnétique ayant une polarisation donnée. Dans ce qui suit, nous emploierons le mot « cible » pour désigner de façon générale un réflecteur ponctuel ou une surface continue.
La figure 1-10 nous aide à comprendre comment un radar polarimétrique nous permet de mesurer les propriétés diffusantes d'une cible. Le système radar éclaire la cible avec une onde incidente (A) que la cible (C) diffuse dans toutes les directions. Le radar capte la partie de l'onde diffusée réfléchie directement vers l'antenne réceptrice (B). Souvent, l'antenne réceptrice et l'antenne émettrice sont coïncidentes - nous parlons alors de radar monostatique -, et nous dirons de l'onde captée qu'elle a été rétrodiffusée. Pouvoir choisir la polarisation de l'onde incidente et mesurer toute la polarisation de l'onde rétrodiffusée, nous apportera plus d'informations sur la cible que si nous effectuons des observations dans une seule polarisation.
|
|
|
Un radar polarimétrique ou radar à quadruple polarisation émet les ondes dans deux polarisations orthogonales et les détecte dans les mêmes polarisations. On choisit souvent les polarisations linéaires horizontale (H) et verticale (V) à partir desquelles on peut créer quatre canaux de réception - HH, HV, VV et VH - dont on mesure l'amplitude et la phase. Les signaux mesurés dans ces quatre canaux donnent toutes les données nécessaires à la mesure des propriétés diffusantes de la cible, c'est pourquoi on dit du radar à quadruple polarisation qu'il est totalement polarimétrique. Les deux canaux des radars à double polarisation ne collectent qu'une partie des informations sur les propriétés diffusantes de la cible.
Polarisations d'un système radar
Comment un système radar émet-il des ondes polarisées? Il est doté d'une antenne conçue pour transmettre et capter des ondes dans une polarisation définie. Les antennes peuvent avoir plusieurs formes : cornets, guides d'ondes, dipôles ou plaques. Dans chaque cas, les propriétés électriques et mécaniques de l'antenne font qu'elles émettent des ondes presque purement polarisées, dont l'orientation et l'ellipticité sont définies à l'avance. Dans les systèmes radar simples, où l'antenne sert à l'émission et à la réception, elle est conçue pour émettre et capter la même polarisation![]() .
.
Pour produire une onde dont on peut modifier la polarisation selon les besoins, il est nécessaire d'émettre des signaux avec des composantes dans deux polarisations orthogonales (polarisation de base). Les deux polarisations de base les plus fréquemment utilisées sont les polarisations linéaires horizontale, H, et verticale, V. Certaines utilisations nécessitent le recours à des polarisations circulaires, les radars météorologiques notamment. Leurs polarisations de base sont dénotées D, pour polarisation circulaire droite, et G, pour polarisation circulaire gauche.
Les systèmes radar plus complexes sont conçus pour émettre et capter les ondes dans plus d'une polarisation. On peut émettre les ondes de différentes polarisations séparément en utilisant un commutateur pour diriger, en séquence, l'énergie vers différentes parties de l'antenne (éléments H et V). Dans d'autres cas, il faut utiliser les éléments simultanément. Par exemple, un signal polarisé circulairement peut être transmis en alimentant simultanément les éléments H et V avec des signaux d'amplitude égale, mais séparés de 90° en phase. (Figure 1 3, supra)
Puisque la diffusion peut modifier la polarisation de l'onde incidente, on conçoit souvent les antennes radar pour qu'elles puissent capter simultanément les différentes polarisations de l'onde. Par exemple, les éléments H et V d'une antenne peuvent capter les deux composantes orthogonales de l'onde réfléchie qui seront traitées séparément par l'électronique du système.
Ainsi, un système radar avec les polarisations linéaires horizontales et verticales pourra avoir quatre canaux :
- HH - émission horizontale, réception horizontale (HH)
- VV - émission verticale, réception verticale (VV)
- HV - émission horizontale, réception verticale(HV), and
- VH - émission verticale, réception horizontale(VH).
On dit des deux premières combinaisons, que les polarisations sont parallèles et des deux dernières qu'elles sont orthogonales.
Un système radar peut présenter différents degrés de complexité du point de vue de la polarisation :
- polarisation simple - HH, VV, HV ou VH
- double polarisation - HH et HV, VV et VH ou HH et VV
- quadruple polarisation - HH, VV, HV et VH
Les systèmes radar à quadruple polarisation (ou radars polarimétriques) utilisent ces quatre polarisations et mesurent les différences de phase entre les canaux, ainsi que les amplitudes. Certains systèmes à polarisation double mesurent la différence de phase entre les deux canaux, donnée essentielle pour l'extraction des informations polarimétriques.
Matrice de diffusion
Lorsqu'une onde polarisée horizontalement frappe une cible, l'onde diffusée peut avoir des composantes horizontales et verticales. Semblablement, la diffusion d'une onde incidente polarisée verticalement aura des composantes dans les deux directions orthogonales. Les composantes horizontale et verticale constituent un ensemble complet permettant de représenter l'onde électromagnétique. De façon analogue, les propriétés de diffusion d'une cible sont contenues en totalité par la matrice de diffusion S qui décrit comment la diffusion transforme le champ électrique de l'onde incidente au champ électrique de l'onde diffusée. La matrice est définie par l'équation :
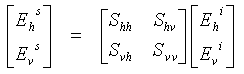 , (5)
, (5)
où l'indice supérieur « i » réfère à l'onde incidente, alors que l'indice « d » désigne l'onde diffusée. Une fois que l'on a mesuré la matrice, on pourra calculer l'amplitude et la polarisation de l'onde diffusée, quelque soit la polarisation de l'onde incidente exprimée par le vecteur [ Ehi , Evi ] .
Les quatre éléments de la matrice de diffusion sont des nombres complexes que l'on peut calculer à partir des amplitudes et des phases mesurées par les quatre canaux d'un radar polarimétrique. On doit utiliser une procédure d'étalonnage précise pour obtenir ces éléments. Toutefois, s'il n'était pas nécessaire d'effecteur cet étalonnage, on pourrait mesurer directement les quatre éléments à partir des canaux correspondants du système radar. Les propriétés diffusantes que l'on a mesurées ne sont valides que pour la fréquence et l'angle de faisceau utilisés pendant la mission. En effet, les propriétés diffusantes varient énormément avec la fréquence du radar et de la direction du faisceau (ou de la rotation de la cible). Ainsi, il faudra choisir prudemment ces paramètres pour qu'ils soient représentatifs du scénario désiré pour les mesures.
Avec les radars monostatiques, la plupart des cibles sont réciproques, ce qui veut dire que Shv = Svh, ou que la matrice de diffusion est symétrique et que seuls trois de ses éléments sont indépendants. On notera que puisque les éléments de la matrice sont complexes, ils tiennent compte de tout changement de phase causé par la diffusion.
Convention pour les coordonnées : L'onde électromagnétique plane se propage dans un espace tridimensionnel décrit par les axes x, y et z. L'axe des z indique la direction de propagation, alors que les axes x et y sont dans le plan perpendiculaire. Les axes (x, y, z) forment un repère orthogonal droit. Dans le cas de la diffusion, on doit définir l'espace des coordonnées pour l'onde incidente et l'onde diffusée.
Les chercheurs utilisent deux conventions : l'alignement « dans le sens de l'onde » et l'alignement « vers la cible ». Dans le premier cas, l'axe z est positif dans la direction de la propagation de l'onde (pour l'onde incidente et l'onde réfléchie). Dans le deuxième, l'axe des z pointe toujours vers la cible (pour l'onde incidente et l'onde réfléchie). (En anglais, on désigne ces deux conventions respectivement par les expressions forward scatter alignment et back scatter alignment, abréviées FSA et BSA). Ainsi, dans les deux conventions, l'onde incidente pointe dans la direction de l'axe des z, mais dans la convention « vers la cible », l'onde diffusée pointe dans la direction opposée. Pour les radars monostatiques, le système de coordonnées est donc le même pour l'onde incidente et l'onde réfléchie dans la convention « vers la cible », c'est pourquoi on adopte habituellement la convention BSA pour les radars imageurs.
La forme de la matrice de diffusion est différente pour l'une ou l'autre convention. Ainsi, en BSA (vers la cible), elle s'appelle matrice de Sinclair, alors qu'en FSA (dans le sens de l'onde), on parle de matrice de Jones ![]() , (page 278).
, (page 278).
Question éclair
Question: Comment la polarisation de l'onde diffusée diffère-t-elle selon que l'on adopte la convention FSA (dans le sens de l'onde) ou BSA (vers la cible)? La réponse...
Question éclair - réponse
Réponse : Dans la convention BSA, on observe l'onde électromagnétique à partir d'un point opposé à celui adopté dans la convention FSA. Ce choix renverse la direction apparente de la rotation de l'onde et, donc, induit un changement de signe pour l'ellipticité de l'onde.
Ellipse de polarisation
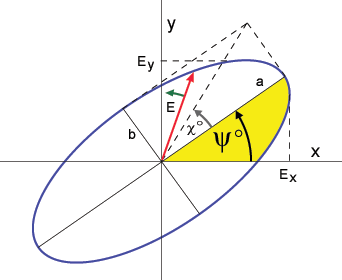
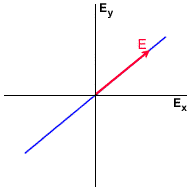
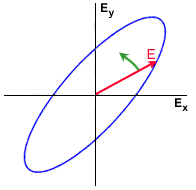
On peut considérer que le champ électrique d'une onde plane est la somme vectorielle de deux composantes orthogonales, habituellement les composantes horizontale et verticale. Ces deux composantes sont caractérisées par leur amplitude et leur différence de phase. Si nous observons l'onde dans la direction de sa propagation, la pointe du vecteur du champ électrique d'une onde complètement polarisée trace une courbe régulière dont la forme la plus générale est l'ellipse. (Cf. figure 1 2).
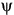 et son ellipticité,
et son ellipticité, 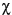 , lesquels sont des fonctions du demi-grand axe, a, et du demi-grand axe, b.
, lesquels sont des fonctions du demi-grand axe, a, et du demi-grand axe, b.L'ellipse possède un demi-grand axe, a, et un demi-petit axe, b. L'angle du demi-grand axe, mesuré dans le sens antihoraire à partir de la moitié positive de l'axe horizontal, est l'orientation, 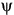 , de l'onde électromagnétique. Sa valeur se situe entre 0° et 180°. L'aplatissement de l'ellipse est décrite par un paramètre nommé ellipticité ou excentricité, défini par
, de l'onde électromagnétique. Sa valeur se situe entre 0° et 180°. L'aplatissement de l'ellipse est décrite par un paramètre nommé ellipticité ou excentricité, défini par 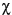 = arctan(b/a). Sa valeur se situe entre -45° et +45°.
= arctan(b/a). Sa valeur se situe entre -45° et +45°.
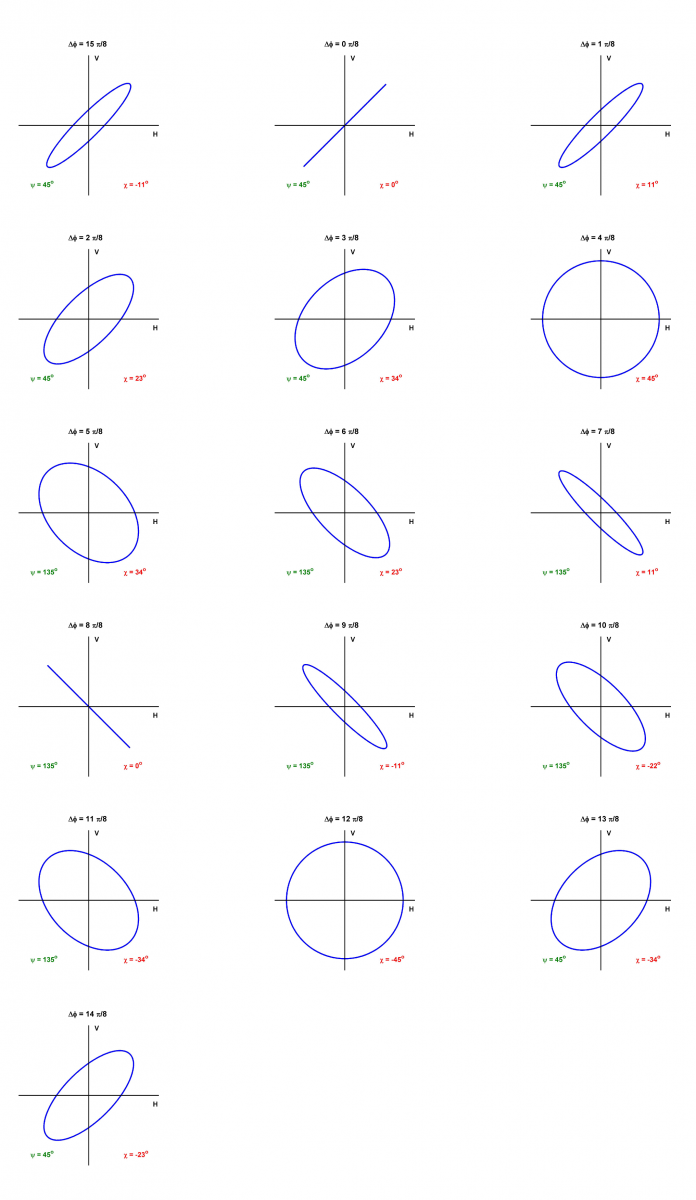
La forme de l'ellipse est régie par l'amplitude et la phase relative des composantes horizontale et verticale du vecteur du champ électrique. La figure 1 3 montre l'effet de la différence de phase entre les composantes pour des amplitudes égales. Lorsque les composantes sont en phase, la polarisation est linéaire (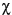 = 0) et l'orientation est de 45°. Si on augmente la différence de phase à
= 0) et l'orientation est de 45°. Si on augmente la différence de phase à 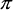 /2 radian, l'orientation demeure à 45°, mais l'ellipticité atteint 45°, l'onde est alors polarisée circulairement. On peut voir cette évolution, par saut de
/2 radian, l'orientation demeure à 45°, mais l'ellipticité atteint 45°, l'onde est alors polarisée circulairement. On peut voir cette évolution, par saut de 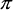 /8 radian, sur la première rangée de la figure 1 3 et la première image de la deuxième rangée.
/8 radian, sur la première rangée de la figure 1 3 et la première image de la deuxième rangée.
Alors que l'on accroît la différence de phase de p/2 à 3p/2 radians, l'orientation passe à 135° et l'ellipticité de +45° à 0° pour atteindre -45°. Cette séquence est visible dans les deuxième et troisième rangées de la figure et la première image de la quatrième. Dans la quatrième rangée, la différence de phase passe de 3p/2 à 15p/8, l'orientation retourne à + 45° et l'ellipticité revient à 0°.
Alors que l'on accroît la différence de phase de 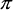 /2 à 3
/2 à 3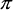 /2 radians, l'orientation passe à 135°, et l'ellipticité de 45° à 0° pour atteindre -45°. Cette séquence est visible dans les deuxième et troisième rangées de la figure et la première image de la quatrième. Dans la quatrième rangée, la différence de phase passe de 3
/2 radians, l'orientation passe à 135°, et l'ellipticité de 45° à 0° pour atteindre -45°. Cette séquence est visible dans les deuxième et troisième rangées de la figure et la première image de la quatrième. Dans la quatrième rangée, la différence de phase passe de 3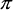 /2 to 15
/2 to 15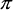 /8, l'orientation retourne à +45°, et l'ellipticité revient à 0°.
/8, l'orientation retourne à +45°, et l'ellipticité revient à 0°.
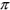 /8 radians par sauts de
/8 radians par sauts de 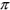 /8
/8Image agrandie
On peut voir à la figure 1-3 que le cercle et le segment de droite sont les cas limites de l'ellipse. Si l'angle de phase entre les composantes horizontale et verticale est 0° ou 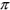 radians, l'ellipse devient une ligne droite. Dans ce cas, l'ellipticité est zéro et la polarisation est linéaire.
radians, l'ellipse devient une ligne droite. Dans ce cas, l'ellipticité est zéro et la polarisation est linéaire.
 Le saviez-vous?
Le saviez-vous?On peut produire une onde totalement polarisée à partir d'un mélange d'ondes sinusoïdales de plusieurs fréquences. Cependant, on suppose généralement dans les systèmes de radar à synthèse d'ouverture qu'il n'y a qu'une seule fréquence, en d'autres termes, que l'onde est monochromatique. Cette hypothèse est valide, puisque ces systèmes ont une largeur de bande très étroite (relativement à leur fréquence) et que l'on peut approximer que l'onde transmise est parfaitement sinusoïdale.
Dans la figure 1-3, les amplitudes des composantes horizontale et verticale sont égales. En cas d'inégalité, l'orientation, 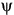 y, peut prendre une valeur entre 0 et 180°. Si l'ellipticité est zéro et l'orientation égale à 0° ou 180°, la polarisation linéaire est horizontale (la composante verticale est nulle). En contrepartie, si
y, peut prendre une valeur entre 0 et 180°. Si l'ellipticité est zéro et l'orientation égale à 0° ou 180°, la polarisation linéaire est horizontale (la composante verticale est nulle). En contrepartie, si 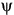 = 90°, l'onde est polarisée linéairement dans l'axe vertical (sa composante horizontale est nulle). On utilise habituellement ces deux polarisations linéaires.
= 90°, l'onde est polarisée linéairement dans l'axe vertical (sa composante horizontale est nulle). On utilise habituellement ces deux polarisations linéaires.
Si l'angle de phase entre les composantes horizontale et verticale est égal à 90°, alors que les composantes horizontale et verticale sont égales, l'ellipse devient un cercle. Dans ce cas, l'ellipticité égale 45° et l'orientation ne peut être définie. Une ellipticité, 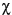 = - 45°, correspond à une polarisation circulaire droite (appelée parfois polarisation dextrogyre). Le vecteur du champ électrique d'une onde polarisée circulairement à gauche, si elle est observée le long de sa propagation, tourne dans le sens antihoraire. (On parle parfois de polarisation lévogyre ou, très rarement, sénestrogyre).
= - 45°, correspond à une polarisation circulaire droite (appelée parfois polarisation dextrogyre). Le vecteur du champ électrique d'une onde polarisée circulairement à gauche, si elle est observée le long de sa propagation, tourne dans le sens antihoraire. (On parle parfois de polarisation lévogyre ou, très rarement, sénestrogyre).
Les figures suivantes montrent les polarisations linéaire, elliptique et circulaire, la rotation du vecteur du champ électrique est aussi illustrée.
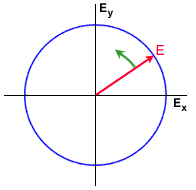
Question éclair

Question: Pourquoi les composantes horizontale et verticale suffisent-elles à décrire la polarisation d'une onde électromagnétique?
Question éclair - réponse

Réponse : La polarisation d'une onde électromagnétique plane est décrite par le lieu tracé par la pointe de son vecteur électrique dans le plan perpendiculaire à sa propagation. Or, dans un plan, deux axes orthogonaux seulement sont nécessaires pour décrire la position d'un vecteur. Les composantes horizontale et verticale Ex et Ey (ou Eh et Ev) sont les plus commodes.
État de polarisation
L'état de polarisation d'une onde plane peut être décrit par l'orientation, l'ellipticité et S0, un paramètre proportionnel à l'intensité totale de l'onde. Pour décrire l'état de polarisation d'une onde électromagnétique, George Gabriel Stokes, physicien irlandais, a introduit un vecteur de quatre éléments, [ S0, Q, U V ] T. Le vecteur de Stokes est défini comme suit :
 (1)
(1)
où Eh et Ev sont les composantes horizontale et verticale de l'onde, S0 est proportionnel à l'intensité totale de l'onde, les deux barres verticales | | désignent la valeur absolue, l'astérisque, *, la conjuguée complexe, ![]() la partie réelle du nombre complexe et
la partie réelle du nombre complexe et ![]() sa partie imaginaire. Une onde électromagnétique plane peut être complètement polarisée, partiellement polarisée ou complètement non polarisée. Pour une onde complètement polarisée, seuls trois paramètres de Stokes sont indépendants, puisque la puissance totale est donnée par :
sa partie imaginaire. Une onde électromagnétique plane peut être complètement polarisée, partiellement polarisée ou complètement non polarisée. Pour une onde complètement polarisée, seuls trois paramètres de Stokes sont indépendants, puisque la puissance totale est donnée par :
![]() (2)
(2)
Comme le montre la figure 1 8, on peut décrire l'état d'une onde complètement polarisée comme un point sur la sphère de Poincaré. Le rayon de la sphère est S0, l’intensité de l’onde. La latitude d’un point sur la sphère correspond à 2![]() , i.e. deux fois l’ellipticité de l’onde.
, i.e. deux fois l’ellipticité de l’onde.
Le saviez-vous?
|
Le rayon de la sphère représente l'intensité de l'onde, S0. Sur la sphère, la latitude correspond à 2![]() , soit deux fois l'ellipticité de l'onde, et la longitude à 2
, soit deux fois l'ellipticité de l'onde, et la longitude à 2 ![]() , soit deux fois l'orientation de l'onde.
, soit deux fois l'orientation de l'onde.
Dans cette représentation, les polarisations linéaires sont sur l'équateur, les polarisations horizontale et verticale étant aux antipodes. Les polarisations circulaires gauche et droite sont respectivement sur les pôles nord et sud. Tous les autres points de la sphère représentent des polarisations elliptiques, d'orientation (![]() ) et d'ellipticité (
) et d'ellipticité (![]() ) différentes. Sur la sphère, les points aux antipodes représentent des polarisations mutuellement orthogonales.
) différentes. Sur la sphère, les points aux antipodes représentent des polarisations mutuellement orthogonales.
On peut décrire une onde partiellement polarisée, comme la somme d'une onde polarisée et d'une onde complètement non polarisée. Le degré de polarisation est le rapport entre la puissance du signal polarisé et la puissance totale, que l'on peut écrire ainsi avec les paramètres de Stokes :
 (3)
(3)
Donc, pour des ondes partiellement polarisées, la puissance totale est supérieure à la puissance polarisée :
![]() (4)
(4)

Figure 1-8: Orientation et ellipticité d'une onde complètement polarisée sur la spère de Poincaré.
Question éclair
![]()
Question: Si une onde électromagnétique est polarisée horizontalement, quelle est la polarisation orthogonale correspondante?
Question éclair - réponse
![]()
Réponse : La polarisation orthogonale correspondante est la polarisation verticale. Deux polarisations orthogonales forment un ensemble de base que l'on peut utiliser pour décrire la polarisation d'une onde électromagnétique. Bien que l'on utilise habituellement les polarisations linéaires horizontale et verticale, on choisit parfois les polarisations circulaires gauche et droite comme polarisations de base.


 Le physicien George Gabriel Stokes est né le 13 août 1819 à Skreen dans le comté de Sligo (Irlande). En 1849, il devenait professeur à Cambridge, poste qu'il occupa jusqu'à sa mort le 1er février 1903 (on vient de célébrer son centenaire). Outre ses travaux sur la polarimétrie et la théorie de la lumière, il est aussi connu pour ses recherches en mécanique des fluides, en analyse spectrale, en géodésie et en théorie acoustique et sur le calcul vectoriel. Élu membre de la Société royale en 1851, il en assuma la présidence de 1885 à 1890. Il siégea également au parlement britannique entre 1887 et 1892, où il fut remarqué pour son soutien aux questions d'éducation.
Le physicien George Gabriel Stokes est né le 13 août 1819 à Skreen dans le comté de Sligo (Irlande). En 1849, il devenait professeur à Cambridge, poste qu'il occupa jusqu'à sa mort le 1er février 1903 (on vient de célébrer son centenaire). Outre ses travaux sur la polarimétrie et la théorie de la lumière, il est aussi connu pour ses recherches en mécanique des fluides, en analyse spectrale, en géodésie et en théorie acoustique et sur le calcul vectoriel. Élu membre de la Société royale en 1851, il en assuma la présidence de 1885 à 1890. Il siégea également au parlement britannique entre 1887 et 1892, où il fut remarqué pour son soutien aux questions d'éducation.